
Exercice donné en classe de troisième en application du théorème de Thales
Soit le triangle ABC. I un point de (AB) et J un point de (AC) tel que (IJ) // (BC). On trace les segments (IC) et (BJ) qui se coupent en un point M. On trace la droite passant par les points A et M qui coupe (BC) en un point K.
Démontrez que K est au milieu de BC

Réponse :
Nous allons démontrer
que le segment (AK) est la médiane du triangle BAC. Nous allons pour
cela démontrer que M appartenant à la droite AK est un point de
la médiane du triangle BAC.
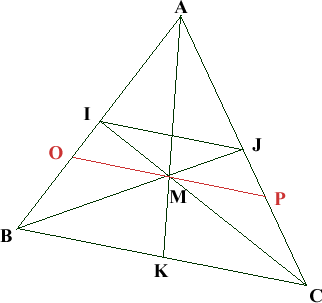
Tout d'abord, on trace un segment (OP) passant par M // à (BC) et (IJ).
 |
O est le
point d'intersection entre (OP) et (AB) Cette droite
(OP) va nous permettre d'utiliser le théorème de Thales
en ayant dans nos égalités (OM) et (MP). Ce que nous ne
pouvions pas faire autrement. (IO) / (IB) = (OM) / (BC) Le théorème de Thales appliqué au triangle BJC (JP) / (JC) = (MP) / (BC) Le théorème
de Thales appliqué aux droites parallèles (IJ), (OP), (BC)
coupés par les segments (AB) et (AC) On peut donc
écrire : On a donc OM = MP. Donc M milieu de OP |
M appartenant au
segment AK implique que AK est la médiane du triangle BAC.
Or, la médiane d'un triangle joint un sommet au milieu du côté
opposé.
| K est donc le milieu de BC |